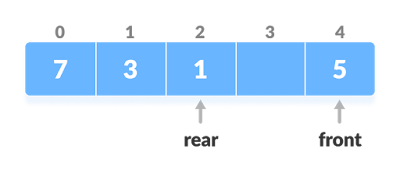
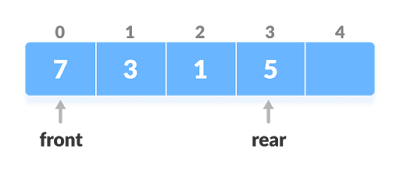
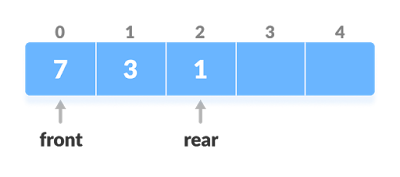
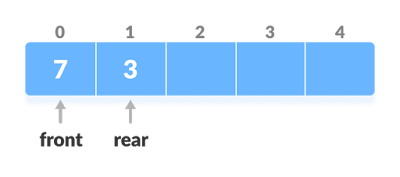
The dequeue stands for Double Ended Queue. In the queue, the insertion takes place from one end while the deletion takes place from another end. The end at which the insertion occurs is known as the rear end whereas the end at which the deletion occurs is known as front end.
Types of Deque
Input Restricted Deque
input is restricted at a single end but allows deletion at both the ends.
Output Restricted Deque
output is restricted at a single end but allows insertion at both the ends.
Operations on a Deque
Below is the circular array implementation of deque. In a circular array, if the array is full, we start from the beginning.
But in a linear array implementation, if the array is full, no more elements can be inserted. In each of the operations below, if the array is full, "overflow message" is thrown.
Before performing the following operations, these steps are followed.
- Take an array (deque) of size n.
- Set two pointers at the first position and set front = -1 and rear = 0.
1. Insert at the Front
This operation adds an element at the front.
- Check the position of front.
- If front < 1, reinitialize front = n-1 (last index).
- Else, decrease front by 1.
- Add the new key 5 into array[front]
2. Insert at the Rear
This operation adds an element to the rear.
- Check if the array is full.
- If the deque is full, reinitialize rear = 0.
- Else, increase rear by 1.
- Add the new key 5 into array[rear].
3. Delete from the Front
The operation deletes an element from the front.
- Check if the deque is empty
- If the deque is empty (i.e. front = -1), deletion cannot be performed (underflow condition).
- If the deque has only one element (i.e. front = rear), set front = -1 and rear = -1.
- Else if front is at the end (i.e. front = n - 1), set go to the front front = 0.
- Else, front = front + 1
4. Delete from the Rear
This operation deletes an element from the rear.
- Check if the deque is empty
- If the deque is empty (i.e. front = -1), deletion cannot be performed (underflow condition).
- If the deque has only one element (i.e. front = rear), set front = -1 and rear = -1, else follow the steps below.
- If rear is at the front (i.e. rear = 0), set go to the front rear = n - 1.
- Else, rear = rear - 1.
5. Check Empty
This operation checks if the deque is empty. If front = -1, the deque is empty.
6. Check Full
This operation checks if the deque is full. If front = 0 and rear = n - 1 OR front = rear + 1, the deque is full.
Deque Implementation in C and Java;
Implementation in C
// Deque implementation in C
#include <stdio.h>
#define MAX 10
void addFront(int *, int, int *, int *);
void addRear(int *, int, int *, int *);
int delFront(int *, int *, int *);
int delRear(int *, int *, int *);
void display(int *);
int count(int *);
int main() {
int arr[MAX];
int front, rear, i, n;
front = rear = -1;
for (i = 0; i < MAX; i++)
arr[i] = 0;
addRear(arr, 5, &front, &rear);
addFront(arr, 12, &front, &rear);
addRear(arr, 11, &front, &rear);
addFront(arr, 5, &front, &rear);
addRear(arr, 6, &front, &rear);
addFront(arr, 8, &front, &rear);
printf("\nElements in a deque: ");
display(arr);
i = delFront(arr, &front, &rear);
printf("\nremoved item: %d", i);
printf("\nElements in a deque after deletion: ");
display(arr);
addRear(arr, 16, &front, &rear);
addRear(arr, 7, &front, &rear);
printf("\nElements in a deque after addition: ");
display(arr);
i = delRear(arr, &front, &rear);
printf("\nremoved item: %d", i);
printf("\nElements in a deque after deletion: ");
display(arr);
n = count(arr);
printf("\nTotal number of elements in deque: %d", n);
}
void addFront(int *arr, int item, int *pfront, int *prear) {
int i, k, c;
if (*pfront == 0 && *prear == MAX - 1) {
printf("\nDeque is full.\n");
return;
}
if (*pfront == -1) {
*pfront = *prear = 0;
arr[*pfront] = item;
return;
}
if (*prear != MAX - 1) {
c = count(arr);
k = *prear + 1;
for (i = 1; i <= c; i++) {
arr[k] = arr[k - 1];
k--;
}
arr[k] = item;
*pfront = k;
(*prear)++;
} else {
(*pfront)--;
arr[*pfront] = item;
}
}
void addRear(int *arr, int item, int *pfront, int *prear) {
int i, k;
if (*pfront == 0 && *prear == MAX - 1) {
printf("\nDeque is full.\n");
return;
}
if (*pfront == -1) {
*prear = *pfront = 0;
arr[*prear] = item;
return;
}
if (*prear == MAX - 1) {
k = *pfront - 1;
for (i = *pfront - 1; i < *prear; i++) {
k = i;
if (k == MAX - 1)
arr[k] = 0;
else
arr[k] = arr[i + 1];
}
(*prear)--;
(*pfront)--;
}
(*prear)++;
arr[*prear] = item;
}
int delFront(int *arr, int *pfront, int *prear) {
int item;
if (*pfront == -1) {
printf("\nDeque is empty.\n");
return 0;
}
item = arr[*pfront];
arr[*pfront] = 0;
if (*pfront == *prear)
*pfront = *prear = -1;
else
(*pfront)++;
return item;
}
int delRear(int *arr, int *pfront, int *prear) {
int item;
if (*pfront == -1) {
printf("\nDeque is empty.\n");
return 0;
}
item = arr[*prear];
arr[*prear] = 0;
(*prear)--;
if (*prear == -1)
*pfront = -1;
return item;
}
void display(int *arr) {
int i;
printf("\n front: ");
for (i = 0; i < MAX; i++)
printf(" %d", arr[i]);
printf(" :rear");
}
int count(int *arr) {
int c = 0, i;
for (i = 0; i < MAX; i++) {
if (arr[i] != 0)
c++;
}
return c;
}
Implementation in Java
// Deque implementation in Java
class Deque {
static final int MAX = 100;
int arr[];
int front;
int rear;
int size;
public Deque(int size) {
arr = new int[MAX];
front = -1;
rear = 0;
this.size = size;
}
boolean isFull() {
return ((front == 0 && rear == size - 1) || front == rear + 1);
}
boolean isEmpty() {
return (front == -1);
}
void insertfront(int key) {
if (isFull()) {
System.out.println("Overflow");
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (front == 0)
front = size - 1;
else
front = front - 1;
arr[front] = key;
}
void insertrear(int key) {
if (isFull()) {
System.out.println(" Overflow ");
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (rear == size - 1)
rear = 0;
else
rear = rear + 1;
arr[rear] = key;
}
void deletefront() {
if (isEmpty()) {
System.out.println("Queue Underflow\n");
return;
}
// Deque has only one element
if (front == rear) {
front = -1;
rear = -1;
} else if (front == size - 1)
front = 0;
else
front = front + 1;
}
void deleterear() {
if (isEmpty()) {
System.out.println(" Underflow");
return;
}
if (front == rear) {
front = -1;
rear = -1;
} else if (rear == 0)
rear = size - 1;
else
rear = rear - 1;
}
int getFront() {
if (isEmpty()) {
System.out.println(" Underflow");
return -1;
}
return arr[front];
}
int getRear() {
if (isEmpty() || rear < 0) {
System.out.println(" Underflow\n");
return -1;
}
return arr[rear];
}
public static void main(String[] args) {
Deque dq = new Deque(4);
System.out.println("Insert element at rear end : 12 ");
dq.insertrear(12);
System.out.println("insert element at rear end : 14 ");
dq.insertrear(14);
System.out.println("get rear element : " + dq.getRear());
dq.deleterear();
System.out.println("After delete rear element new rear become : " + dq.getRear());
System.out.println("inserting element at front end");
dq.insertfront(13);
System.out.println("get front element: " + dq.getFront());
dq.deletefront();
System.out.println("After delete front element new front become : " + +dq.getFront());
}
}
Applications of Deque
- The deque can be used as a stack and queue; therefore, it can perform both redo and undo operations.
- It can be used as a palindrome checker means that if we read the string from both ends, then the string would be the same.
- It can be used for multiprocessor scheduling. Suppose we have two processors, and each processor has one process to execute. Each processor is assigned with a process or a job, and each process contains multiple threads. Each processor maintains a deque that contains threads that are ready to execute. The processor executes a process, and if a process creates a child process then that process will be inserted at the front of the deque of the parent process. Suppose the processor P2 has completed the execution of all its threads then it steals the thread from the rear end of the processor P1 and adds to the front end of the processor P2. The processor P2 will take the thread from the front end; therefore, the deletion takes from both the ends, i.e., front and rear end. This is known as the A-steal algorithm for scheduling.
For Videos Join Our Youtube Channel: Join Now
